Álgebra desde Barra de Entrada-Comandos y Funciones(compendio)

Dando Entrada a Objetos de Definición Algebraica
1. Se les da Nombre a Nuevos Objetos, simplemente anteponiendo su nombre = en la Barra de Entrada a su definición algebraica.
2. Un Producto se establece con un asterisco o espacio entre los factores.
x(P_1) * x o x(P:1) x
3. ¡GeoGebra es sensible a las minúsculas diferencias!... lo que implica que identifica como distintos los nombres de variables en que solo una mayúscula o un tilde distingue una de otra. Por eso es preciso controlar estas cuestiones tanto al otorgar un nombre como al referirlo.
- Los nombres que otorga GeoGebra, espontáneamente a los objetos creados - sea a partir de una herramienta como desde un comando - presentan ciertas distinciones y así, los de los...
- Puntos son letras mayúsculas. Ejemplo: A = (1, 2) o, en coordenadas polares, B = (2; pi)
- Vectores son letras minúsculas Ejemplo: v = (1, 3)
 Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
Aviso: Si se asignara la misma definición de valores a objetos anotados con minúsculas - como a o b -, GeoGebra los establecería como vectores posición de puntos de coordenadas (1, 2) o (2; pi) respectivamente.
- Puntos son letras mayúsculas.
- Llevan minúsculas también las...
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados Ejemplo: circunferencia c: (x – 2)^2 + (y – 1)^2 = 16
- Circunferencias (así como los arcos y las cónicas), rectas (así como los segmentos y semirrectas), funciones y otros elementos asociados
- Deben anotarse y referirse en minúsculas los nombres de las variables como...
- la independiente x de una función o
- x e y en cualquier expresión - ecuación de una sección cónica, de una inecuación, etc. -. Ejemplo: f(x) = 3*x + 2
4. Para incluir un objeto en una anotación en la Barra de Entrada, es preciso crearlo antes y referirlo por el nombre que lo identifica, recordando distinguirlo con todos los detalles correspondientes (mayúsculas, minúsculas, tildes...). Esto vale tanto para las expresiones algebraicas como para los comandos...
- y = m x + b o y = m f(-b) x + f(b) crea una recta en tanto m como b sean ya:
- números que harán las veces de parámetros (recordar que todo número establecido como tal involucra un deslizador cuyo valor puede modificarse en tanto se lo torne visible en la Vista Gráfica activa.
- Recta(A, B) o Recta(A + b Vector(A, B) , B) crea una recta en tanto exista el punto A y el B y/o el número b.
5. Cada expresión ingresada en la Barra de Entrada se debe confirmar' pulsando la tecla Enter (o Intro como aparece en algunos teclados).
6. Tanto la tecla de atajo (F1) como la opción de Ayuda del Menú o el Manual, permiten abrir la ventana pertinente para averiguar el modo de empleo de un comando en la Barra de Entrada.
7. Si al ingresar un comando en la Barra de Entrada aparece un error, conviene leer detenidamente el correspondiente mensaje para tener mayores recursos para subsanarlo.
8. Los Comandos se pueden anotados o seleccionados desde la lista próxima a la Barra de Entrada.
9. Tras anotar las dos primeras letras de cualquier comando en la Barra de Entrada, emergen alternativas para su Completado Automático tentativo que permite...
- Seleccionar el adecuado pulsando Enter ( Intro en algunos teclados) para ubicar el cursor entre los corchetes.
- Proseguir anotando las siguientes letras hasta que se despliegue el deseado.
Construyendo Circunferencias Suponiendo sus Tangentes
¿Por qué no realizar el trayecto de regreso desde las construcciones convencionales imaginando un desafío inverso en que se pueda tantear dinámicamente como medio legítimo para dar con conjeturas a controlar y validar? Imaginemos que la consigna fuese la siguiente:
- Dicen que había una circunferencia a la que se le trazaron las tangentes desde A y B. Esos puntos exteriores son todo lo que ha perdurado de esa antiquísima construcción ya desvaída.
- Algunos creen recordar que esas cuatro tangentes conformaban un específico cuadrilátero.
- El desafío es establecer, más allá de lo que circula en los rumores o de lo que sostienen los que se consideran dignos memoriosos...
- qué tipo de cuadrilátero podría haber sido
- cómo descartar los que no tendrían chance alguna de haber quedado trazados.
Esbozando Alternativas
Aceptado que fuera el desafío, es posible que se intente empezar a pensar sobre un diagrama hacia una figura de análisis. El instructivo que se detalla a continuación permite esbozar una. Antes de adoptarla, conviene idear las propias y, para realizarla con GeoGebra, consultar el manual en relación a las herramientas que se requieran.
Especulaciones hacia y desde la Figura de Análisis
Consideraciones Iniciales
- Algunos aseguran que sin necesidad de reconstruir lo que ese diagrama podría haber configurado, pueden descartarse algunos cuadriláteros desde ya,
- Señalan, por ejemplo, la imposibilidad de...
- todo trapecio
- los rectángulos en general
- los rombos en particular
- Otros sostienen que no es dable descartar ninguno de entrada y que es conveniente comenzar por una figura de análisis retrospectivo para empezar. Valdría cuestionarse si...
- ¿Se puede justificar una u otra posición?
Desafío guiando al Tutorial
Se lista un instructivo para desarrollar un boceto según una modalidad que surgió en un Taller, reiterando esta es apenas una alternativa a la que conviene sumar las que propongan quienes reformulen y recaben ideas de otros, participantes o diseñadores que ajusten el desafío.
Rastros para una Construcción Retrospectiva
Avanzando en la Construcción Retrospectiva
Sobre la Figura de Análisis
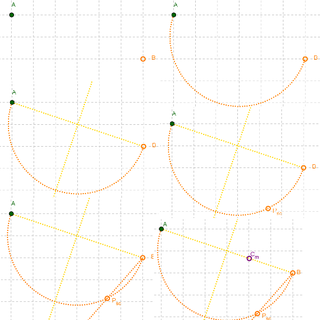
Como los puntos A y B establecen los datos dados, debieran permanecer fijos en el diagrama que se trace.
- En la construcción que se propone se puede modificar la posición:
- del centro de la presunta circunferencia y
- la del punto que, sobre la semicircunferencia entre A y B, establece la dirección de la primera de las tangentes.
Este interjuego de resultados de los desplazamientos de esos dos puntos deslizables ofrece un banco de pruebas dinámico.
- La exploración se limita a desplazar los puntos...
- C_m (que opera como centro de la presunta circunferencia que se intenta reconstruir) y
- P_{sc} que, sobre la semicircunferencia desde A a B, determina el sentido de la primera tangente.
- A partir de los ensayos, se podría reconsiderar si...
- el tanteo sistemático permite distinguir lo que efectivamente se pudiera descartar de entrada de lo que no puede determinarse a menos que se brinden más datos.
- Desde la perspectiva operativa, si...
- podrían emplearse herramientas o maniobras alternativas para recrear la construcción
- hay medios para controlar si el cuadrilátero delimitado por las cuatro presuntas tangentes constituye uno de algún tipo específico
- se evidencian relaciones entre los elementos que se distinguen como propiedades exclusivas de un tipo de cuadrilátero.
- En cuanto a la potencia de las exploraciones, conviene cuestionarse si se pueden realizar ensayos exhaustivo modificando la posición de un punto por vez. Por ejemplo,
- ¿el punto que opera como centro de la presunta circunferencia se desplaza convenientemente para indagar en relación a los distintos cuadriláteros sin necesidad de modificar la posición del que se emplea para tantear la dirección de la primera de las tangentes?
- ¿pueden establecerse los tipos de cuadriláteros imposibles dadas las condiciones o la construcción en juego restringe y aparenta la inviabilidad de lo que en otra podrían lograrse? o
- si se partiera de otro tipo de construcción, ¿sería posible dar con otros tipos de cuadriláteros que en la planteada no parecen viables?.
Comandando la Construcción
Definiciones en el Protocolo de Construcción
Si bien el tutorial parece estar basado exclusivamente en las herramientas disponibles, podría haber sido desarrollado sin siquiera apelar al ratón o mouse y / o cualquier dispositivo de contacto dado que se podrían preparar todos los archivos de GeoGebra ingresando los datos respecto de los objetos y anotando los correspondientes comandos en la Barra de Entrada.
El ingreso de datos algebraicos y de comandos supera y amplia el empleo de las herramientas geométricas.
Pruebas y Preparativos
- Abrir una nueva ventana de GeoGebra.
- Exponer la Vista Algebraica y la Barra de Entrada así como la cuadrícula (sea desde el Menú Vista o apelando a los íconos de cada Barra de Estilo según corresponda).
- Seguir paso a paso las indicaciones del Protocolo de Construcción intentando intercalar el empleo de herramientas y el ingreso de los comandos correspondientes en la Barra de Entrada.
Controlar y Explorar la Construcción
- Controlar que los únicos puntos que se pueden desplazar (además de A y B que son datos dados y no debieran moverse como no sea para cambiar las condiciones iniciales), sean los que determinan el centro de la presunta circunferencia y el que, sobre la semicircunferencia, fija el sentido de la primera tangente tentativa.
- Someter la construcción a la prueba de arrastre para verificar que si bien se modifica, las relaciones que se establecieron no se alteran y el rol de los elementos en juego perdura correctamente.
- Cambiar las propiedades de los objetos para ilustrar mejor las relaciones y distinguir los elementos claves así como para mejorar la apariencia de la construcción (por ejemplo, seleccionando los colores armoniosamente, distinguiendo con trazos punteados los elementos auxiliares ,…)
- Guardar la construcción que lleva a la resolución del desafío con un nombre adecuado.
Explorando Relaciones entre Coeficientes y Gráficas en Cuadráticas
En esta propuesta se procurará vincular en sentido directo e inverso, las relaciones entre los coeficientes de una expresión cuadrática y su comportamiento gráfico.
Desafío Reconstructivo
Dados cinco puntos distribuidos al azar, ¿cómo se podría deslizar la gráfica de y = x^2 usando las teclas flecha ascendentes / descendentes y las laterales a izquierda y derecha para que la gráfica cruce por la mayor cantidad de tales puntos?
Preparativos
1 Seleccionar la de Álgebra y Gráficos en el Menú Apariencias
2 Ingresar en la Barra de Entrada, cinco veces esta anotación para dar con puntos al azar:
- (-5 + round(10random()), -4 + round(10random()))
Recordar que con las teclas Alt + Arriba / Alt + Abajo se puede navegar por la historia de comandos ingresados.
Planteo Aleatorio Puntual
Para completar el planteo del desafío que va a guiar la tarea que relaciona los distintos registros - expresión, ecuación, tabla de valores, representación gráfica... - se pasa a considerar la distribución de los puntos: - ¿Conforman un conjunto aceptable del que se puedan elegir cuatro - o al menos tres - para encontrar una cuadrática que los atraviese?
- Decidir si se van a aceptar como datos los cinco puntos que el azar deparó y...
- pulsar las teclas Ctrl + R para que el recálculo de los valores aleatorios provoque una reubicación de los puntos en caso de no estar en una posición adecuada para las condiciones del problema
- copiar las coordenadas de cada punto en un sector de la Hoja de Cálculo que se expondrá con tal fin
- darle a cada punto vistoso y diverso formato y color
3 Ingresar en la Barra de Entrada la siguiente expresión:
- y = x^2
4 Seleccionar la expresión y...
- pulsar las teclas Arriba / Abajo u las Izquierda / Derecha
- registrar el efecto que estas maniobras tienen sobre el gráfico y la expresión correspondiente.
5 Establecer alguna estrategia para lograr que la cuadrática cruce por la mayor cantidad posible de puntos.
Una forma más precisa de cambiar coeficientes y comportamiento de una gráfica cuadrática es anotarla de modo que quede asociada a tres
Coeficientes Deslizables
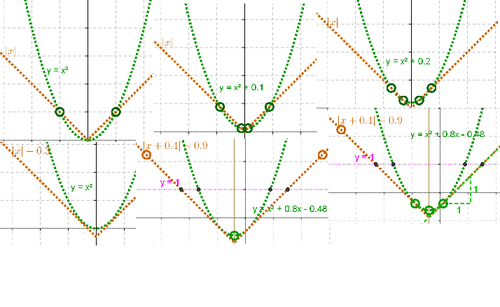
Para contar con una gráfica que sea posible ajustar a la que atraviese la mayor cantidad de puntos aleatorios distribuidos, además de la que originalmente se ingresó como y = x^2 y que se puede maniobrar con las teclas de flecha, basta con...
- Ingresar sucesivamente en la Barra de Entrada, los valores de partida para a, b y c. Como, por ejemplo
- a = 1 y Enter (Intro en algunos teclados)
- con la misma maniobra, ingresar los valores para b y c - por el momento, b=0 y c = 0 -
- Anotar la expresión dependiente de a, b y c...
- a x^2 + b x + c - - a la que se le puede otorgar un color y estilo que la distinga de la previamente ingresada y = x^2 -
- Dar visibilidad a los números a, b y c con un clic en cada redondelito que aparece a la izquierda de cada uno de ellos en la Vista Algebraica.
Ensayos Preliminares
Pueden llevarse adelante algunos ensayos para corroborar que...
- la gráfica de la expresión ingresada - a x^2 + b x + c - reacciona a los cambios en los valores de los deslizadores como se observa en el registro algebraico en que aparece como Objeto Dependiente expresada como f(x) = a x^2 + b x + c
En cambio...
- mantiene su carácter de objeto libre la que fuera originalmente anotada como y = x^2" y cambia su representación gráfica y expresión cuando se la selecciona y se opera con las teclas de flecha
Con una y/u otra gráfica se puede procurar una vía sistemática para lograr que cruce por la mayor cantidad de puntos en juego.
Repertorio de Funciones
Más allá de los polinomios que pueden ingresarse directamente en la Barra de Entrada, es posible apelar a cualquier de los diferentes tipos de funciones disponibles en GeoGebra (sean las trigonométricas, las exponenciales, las de valor absoluto, módulo o resto...). Con las funciones se puede operar como con cualquier otro objeto e incluso combinarse con construcciones geométricas o con datos que se registren en las celdas de una Hoja de Cálculo.
Desafío Absoluto
El siguiente problema vincula las funciones previamente tratadas en un desafío integrador:
- ¿Cómo harían para encontrar una parábola tal que resulten tangentes en algún par de puntos de la correspondiente cuadrática sendas ramas de la gráfica de una función de valor absoluto?
Para encontrar al menos una manera de ilustrar el desafío, conviene...
1 Abrir una nueva ventana de GeoGebra y seleccionar del Menú Apariencias una que incluya la Vista Algebraica, Barra de Entrada y ejes de coordenadas.
2 Preparar al menos tres deslizadores para afectar a la función de 'valor absoluto` para poder ingresarlo como k abs(n x + m), por ejemplo y, a su vez, ingresar otra versión, libre y por tanto desplazable con las teclas de flecha, completamente despojada - abs(x) -.
3 Otro tanto para afectar a la cuadrática a x^2 + b x + c que deberá distinguirse con diferente color y/o estilo que se ingrese, libre y desplazable sin mediaciones, como y = x^2
4 Ocultar el par de funciones que dependen de los deslizadores para encarar el desafío, por empezar, con tanteos sistemáticos que afecten a sendos gráficos libres - y = x^2 y y = abs(x) -
Tanteando Interpretaciones
| 1 | f(x) = abs(x) | Se ingresa la función de valor absoluto para explorar su comportamiento. |
| 2 | y = 3 | Se ingresa la función constante, que aparece con el nombre 'g en el gráfico para indagar todo lo posible, al ir desplazándola, respecto de las relaciones que vinculan a los puntos de intersección con abs(x). |
| 3 | Se trazan los puntos de intersección entre la función abs(x) y la constante paralela al EjeX | |
| 4 | Se traza la mediatriz entre sendos puntos de intersección para poner en evidencia que obra como eje de simetría de esta función. Esta misma maniobra se puede llevar adelante con la parábola para obtener, no solo el eje de simetría sino también el valor de las coordenadas y la posición del vértice. |
Guiando las Primeras Exploraciones
(a) Al desplazar la función constante con el ratón o mouse o empleando las teclas de flechas, se modifican los valores y posiciones de los puntos de intersección. Las ordenada de cada uno de ellos representa el valor absoluto de la abscisa.
(b) Al realizar las mismas maniobras de desplazamiento sobre la función de valor absoluto, pueden registrarse y procurar interpretar los cambios provocados en la ecuación de la función. Es posible solicitar que se pongan en evidencia los vínculos entre estos cambios para completar la apreciación de la función desde sus diversos registros y correlacionarlos.
(c) Estas primeras maniobras que se asocian al propósito central del desafío pero conservan una índole de exploración hasta cierto punto, libre, suele poner en evidencia cuestiones como la de simetría. Característica vinculada a un eje de simetría que, aunque parece surgir a simple vista, solo cobra entidad desde una apreciación más completa, cuando se gana cierta familiaridad con las propiedades implicadas en tanto se las pone en juego como herramientas. Máxime cuando se lo puede provocar como concepto una vez que surgió revitalizado en una comparación - en este caso con la parábola - en relación a un propósito guía.
Actividad Desencadenada por la Consigna
Si cada diseño de situación vale lo que cuesta, lo que debiera distinguirse es si esta desencadena un quehacer matemático compartido más que la de la presentación de los temas que involucra, a identificar e institucionalizar en cada recapitulación tanto operativa como conceptual que jalone las etapas.
Resolución Complementando Registros y Recursos
La secuencia de imágenes ilustra los tanteo que jalonaron una de las exploraciones que se realizaron en paralelo en distintos equipos de trabajo, con mediación para compartir hallazgos:
- los valores de las coordenadas
- la condición de indefinido que los afecta.
- el patrón de resultados por los que se cicla en los intentos desplazando una u otra función (al menos, a lo largo del 'EjeY
1 Se pasa de no tener ningún punto de contacto a tener dos de intersección.
2 Procurando tantear para dar con lo pedido por la consigna, se llegan a cuatro puntos de intersección.
3 Se logran cuatro puntos o ninguno, en una situación que no parece tener mejor salida.
Indicadores y Condiciones
Estas idas y venidas por un ensayo y error que parece servir para configurar un panorama dinámico del funcionamiento de las relaciones en juego pero no alcanzar para alcanzar el propósito, develan la necesidad...
- de contar con indicadores más propicios para guiar la tarea y se opta por sumar al tanteo, dándole visibilidad, a...
- la función constante - en lila en las ilustraciones - para ubicar sus puntos de intersección - en negro en las ilustraciones - con una una y otra gráfica.
- las mediatrices entre
 cada par de esos puntos de intersección, para obtener sendos ejes de simetría.
cada par de esos puntos de intersección, para obtener sendos ejes de simetría.
4 Se identifica el vértice como la intersección de la parábola con el eje de simetría coincidente con la mediatriz correspondiente (de color naranja en el ilustración).
- de controlar algunas condiciones para el logro como la de la coincidencia de los ejes de simetría
- apelando en caso parecer que se superponen, a la
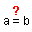 correspondiente herramienta - aplicada a las formulaciones de ambas mediatrices en la Vista Algebraica para evitar la dificultad de la maniobra en la Vista Gráfica - cuando cunde la convicción de no ser suficiente con hacerlo a ojo
correspondiente herramienta - aplicada a las formulaciones de ambas mediatrices en la Vista Algebraica para evitar la dificultad de la maniobra en la Vista Gráfica - cuando cunde la convicción de no ser suficiente con hacerlo a ojo
- apelando en caso parecer que se superponen, a la
- de incluir...
- la tangente a la parábola
 por uno de los puntos de la parábola para guiar el tanteo hacia la situación en que coincida con la correspondiente rama de la función de valor absoluto.
por uno de los puntos de la parábola para guiar el tanteo hacia la situación en que coincida con la correspondiente rama de la función de valor absoluto. - un
 punto que pudiera desplazarse por la parábola - y otro por la función de valor absoluto - de modo de tantear y controlar con mayor facilidad la posición que debía ocupar la tangente para coincidir con una de las ramas de la función de valor absoluto. (Punto de color naranja en la ilustración, por el que se trazó la tangente a la parábola).
punto que pudiera desplazarse por la parábola - y otro por la función de valor absoluto - de modo de tantear y controlar con mayor facilidad la posición que debía ocupar la tangente para coincidir con una de las ramas de la función de valor absoluto. (Punto de color naranja en la ilustración, por el que se trazó la tangente a la parábola). - sendos puntos de reflexión por los correspondientes ejes de simetría
 de cada uno de los puntos móviles que se ubicaron sobre la parábola y la función de valor absoluto. (Puntos de color naranja sobre las ramas derechas, en la ilustración).
de cada uno de los puntos móviles que se ubicaron sobre la parábola y la función de valor absoluto. (Puntos de color naranja sobre las ramas derechas, en la ilustración).
- la tangente a la parábola
5 Se trazan la pendiente a la tangente a la parábola en el punto naranja móvil que se puede desplazar por esa curva.
6 Para poder establecerla también sobre la rama derecha de la función de valor absoluto, se marca otro punto adicional al naranja móvil allí ubicado y para unirlos ![]() con la Herramienta de Recta y poder operar efectivamente sobre una recta.
con la Herramienta de Recta y poder operar efectivamente sobre una recta.
Recién entonces, quien mediaba la situación hubo de intervenir para brindar información sobre las herramientas y las maniobras pertinentes para operar en tal sentido.
7 Tanto la tangente a la parábola como la recta que se traza sobre dos puntos de la rama derecha de la función de valor absoluto, se pasan a exponer con el formato que, ofrecido como alternativa en el Menú Contextual, se aprecia como el más adecuado (para que el primer coeficiente coincida con sus correspondientes pendientes - m- ).
Ida y Vuelta de Herramientas a Objetos
En este contexto, surgió como herramienta operativa lo que llegaría a recuperarse a nivel conceptual, la asociación entre el régimen de variación de la pendiente de la tangente en cada punto de la cuadrática y su derivada, revitalizado como objeto.
Más aún, el contexto de búsqueda de la resolución, llegaría a dar razón de ser a su estudio, incluyendo el retorno a la ecuación de la cuadrática con los deslizadores (a, b y c) o a un tanteo sistematizado de las dos alternativas libres- para completar el quehacer matemático en juego.
8 Para facilitar el acceso a una solución posible, se reitera tanto para la parábola como para la función de valor absoluto, sus formulaciones originales - f(x) = abs(x) y x^2- .
Esto, aunque parezca evidente a los ojos de docentes que recorren la crónica tutorial retrospectivamente, no lo era con suficiente anticipación desde la perspectiva de quienes se encargan de la resolución.
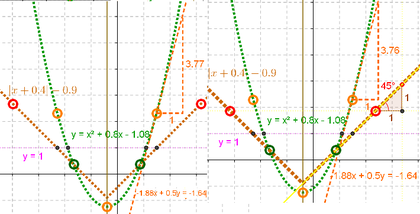
9 Se restablece la situación inicial de tanteo - en que la parábola vuelve a ser x^2 y f(x) = abs(x) la función de valor absoluto que, ajustada pasa a ser abs(x) - 0.25 - .
10 Cuando el tanteo es ya tan sistemático como acotado, se pone en evidencia que lo más ágil resulta colocar el punto desplazable naranja sobre la parábola - vía doble clic en su definición en la Vista Algebraica -en coordenadas tales que la pendiente en la ecuación de la recta tangente - 2 x - resulte igual a la unidad - (0.5, 0.25) _ en este caso -.
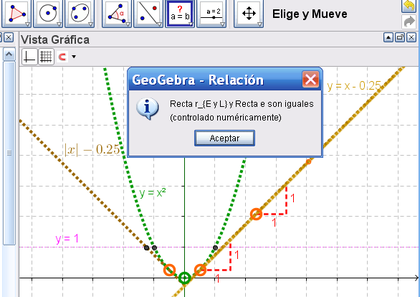
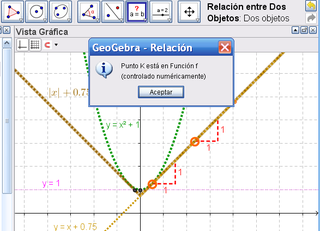
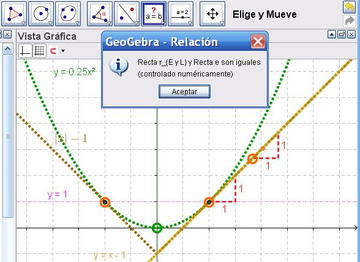
11 Para corroborar con mayor precisión el logro del propósito, se acude nuevamente a la ![]() Herramienta de Relación para controlar que, no ya paralelas sino iguales, resultan las rectas correspondientes a la tangente de la parábola en el punto - (0.5, 0.25) - y la recta que coincide con la rama derecha de la función del valor absoluto - abs(x) - 0.25 - .
Herramienta de Relación para controlar que, no ya paralelas sino iguales, resultan las rectas correspondientes a la tangente de la parábola en el punto - (0.5, 0.25) - y la recta que coincide con la rama derecha de la función del valor absoluto - abs(x) - 0.25 - .
¿Una Solución?, ¿Cuántas Soluciones?
Es conveniente preguntarse por otras posibles una vez que se arriba a una solución válida - su validez puede corroborarse con diferentes estrategias que, en todos los casos, superen el control a ojo de buen cubero que es un valioso recurso que sirve para empezar pero no alcanza para concluir-.
Cada traslación que se realiza tanto sobre la parábola de la solución inicial - x^2- como la de la función de valor absoluto con la que se llegó a ese primer resultado - abs(x) - 0.25 - , también arrastra a todos los elementos, auxiliares o centrales, de la construcción de modo que...
- se llega dinámicamente a una nueva solución tal como se puede controlar con precisión numérica
- registrar a partir de la información expuesta en la Vista Algebraica, susceptible de control algebraico relativamente simple (asociado de tener interés disciplinar y didáctico en el tema a partir de operaciones con la primera derivada de la parábola, pero sin requerir esta tarea).
La cuestión que se despliega es, entonces, ¿cuántas soluciones habrá, más allá de las que se pongan en descubierto en cada traslación conjunta a lo largo del EjeY y/o del EjeX?, ¿serán numerosas o... infinitas?.
Infinitas pero ¡no arbitrarias!
Las traslaciones de la construcción llevan a encontrar otras, semejantes, soluciones.
Considerar la influencia de los cambios en los deslizadores sobre la cuadrática - aquella a x^2 + b x + x dejada de lado en la primera etapa de tanteos - permite distinguir la influencia, no ya de trasladar la parábola sino de modificarla, sobre la índole de la familia de soluciones posibles.
A diferencia de lo provocado por las traslaciones, los cambios en la parábola desde su coeficiente principal, alteran de modo diverso (acaso proporcional), la distancia entre vértices de sendas funciones y las coordenadas del punto en que se encuentra esa tangente coincidente con una rama de la función de valor absoluto.
Cuestiones Motivadas
La motivación desencadenada, lleva a incursionar en...
- el esquema de mecanismos de resolución
- el entrecruzamiento de informaciones y representaciones en diversos registros - gráfico y algebraico fundamentalmente -
- el análisis de los elementos del escenario y contexto del planteo:
- con el consiguiente estudio de la función cuadrática y de la de valor absoluto
- así como el de régimen de variación de cada una de ellas, vinculado a la derivada - como herramienta mientras se perfila como objeto - o, al menos, a su representación gráfica.
... y, sobre todo, en las particularidades del quehacer matemático cruzado por este tipo de herramientas.
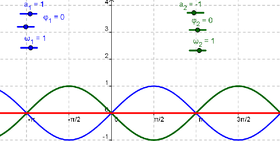
Desafío Periódico
Las ondas de sonido pueden ser matemáticamente representadas como una combinación de sinusoides. Cada nota musical está compuesta de varia sinusoides de formulación y(t) = a sin(ω t + φ) . La amplitud a afecta el volumen y la frecuencia angular ω determina el timbre. El parámetro φ se denomina fase porque la indica en la onda de sonido.
Si dos sinusoides se superponen, interfieren entre sí de modo tal que una amplifica o reduce la amplitud de la otra. Es posible representar este modelo de estudio del fenómeno para examinar casos especiales.
Propuesta
Más allá de estas alternativas en las que podría ahondarse, en este caso apenas se plantea, dadas dos sinusoides obtener su suma y pasar a jugar con sus coeficientes para:
- dar respuesta a algunos interrogantes sobre el efecto de cada coeficiente
- lograr como resultante, un diseño ondulado original para el estampado de tela de tapicería.
Como desafío colateral, se propone indagar si podría resultar una función:
- no periódica o
- de un período mayor o menor que el de sendas sinusoides ingresadas.
Interrogantes
- La resultante de sumar ambas sinusoides, ¿será siempre una función periódica?
- El período de la resultante, ¿podrá ser menor o mayor que el de ambas componentes?
Preparando Coeficientes y Primer Sinusoide
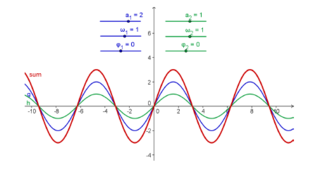
| 1 | Crear tres deslizadores a_1, ω_1, y φ_1 con valores iniciales 1, 1 y 0 respectivamente. | |
| 2 | g(x)= a_1 sin(ω_1 x + φ_1) | Ingresar a continuación la función seno g |
(a) Examinar el impacto de los parámetros - cambio de los valores de los deslizadores - sobre el gráfico de la función sinusoidal. (b) Anticipar el resultado de...
- redefinir g(x) como:
- g(x)= x sin(ω_1 x + φ_1) y como
- g(x)= (1/x) sin(ω_1 x + φ_1)
- corroborar las presunciones con los correspondientes ensayos
- volver a la definición original de g(x) - g(x)= a_1 sin(ω_1 x + φ_1) -
Sumando Sinusoides
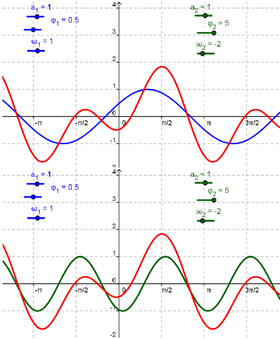
| 3 | Crear tres deslizadores a_2, ω_2, y φ_2 | |
| 4 | h(x)= a_2 sin(ω_2 x + φ_2) | Ingresar la otra función seno - h - |
| 5 | sum(x) = g(x) + h(x) | Anotar la suma de ambas funciones en la Barra de Entrada |
(b) Cambiar el color de las tres funciones para distinguirlas con más facilidad.
(c) Fijar a_1 = 1, ω_1 = 1, y φ_1 = 0.
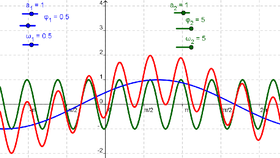
(d) Operar sobre los deslizadores para dar respuesta a los siguientes interrogantes:
- Buscar valores de a_2, ω_2, y φ_2 que afecten a la suma de distintas formas.
- Para que module la amplitud de g(x) a lo largo de todo su período.
- Para que la onda de salida tenga amplitud nula.
- Para que su amplitud sea máxima
 Atención: En este caso, si se tratara de ondas de sonido, el tono resultante tendría volumen máximo.
Atención: En este caso, si se tratara de ondas de sonido, el tono resultante tendría volumen máximo.
- ¿Para cuáles las dos funciones se cancelan mutuamente?
 Atención: En este caso, si se tratara de ondas de sonido, el tono dejaría de ser audible.
Atención: En este caso, si se tratara de ondas de sonido, el tono dejaría de ser audible.
- Nota:
Para profundizar y ampliar lo que se estudia en este tutorial, es aconsejable consultar:
Álgebra desde la Barra de Entrada I
Álgebra desde la Barra de Entrada II
Álgebra desde la Barra de Entrada III y
Álgebra desde la Barra de Entrada IV