Comando Hipergeométrica

De GeoGebra Manual
Hipergeométrica
Categorías de Comandos (todos)
- Hipergeométrica[ <Tamaño de Población>, <Número de Éxitos>, <Tamaño de Muestra> ]
- Establece el histograma de esa distribución hipergeométrica (hypergeometric en inglés).
Parámetros en un ejemplo de bolillas negras exitosas: - Tamaño de Población: número de bolillasen la urna
- Número de Éxitos: número de negrasen la urna
- Tamaño de Muestra: número de las extraídas
El histograma expone la función de probabilidad del número de bolillas negras en la muestralas extraídas.
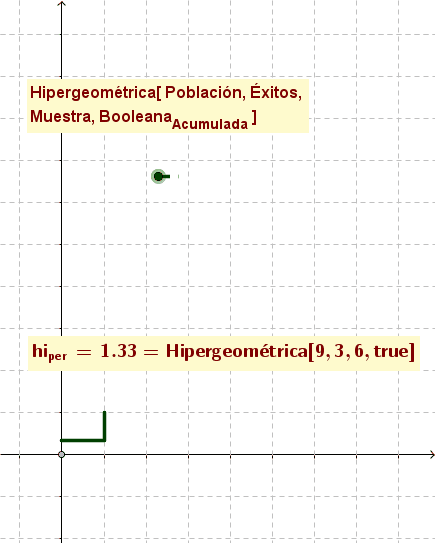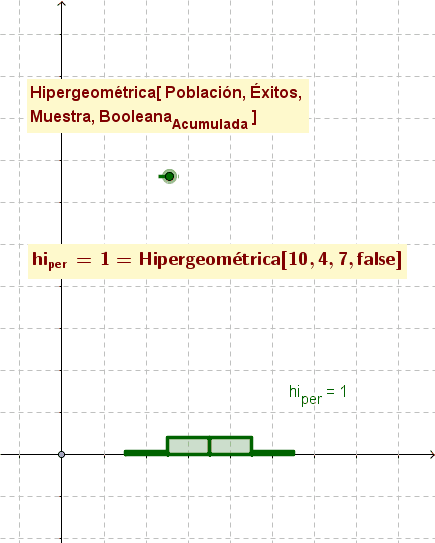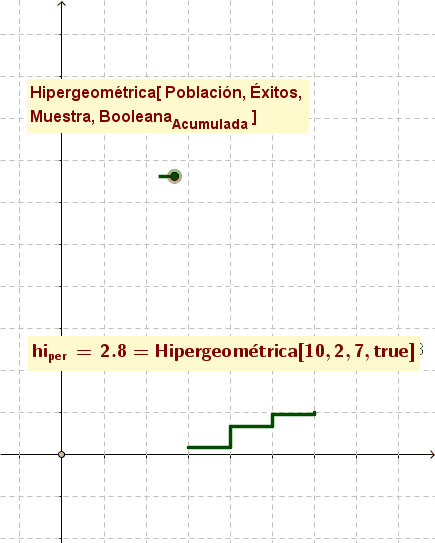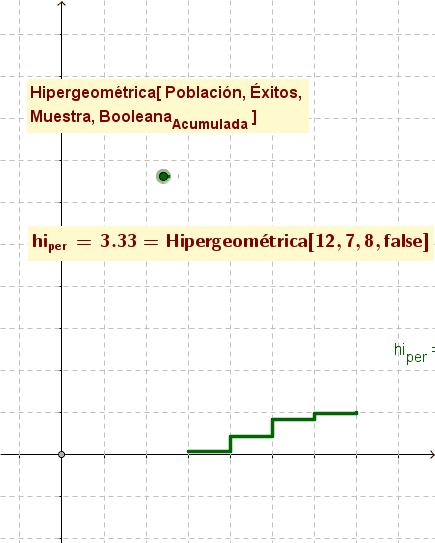
- Hipergeométrica[ <Población>, <Éxitos>, <Muestra>, <BooleanaAcumulativa> ]
- Como en el caso anterior, se establece el histograma de la distribución hipergeométrica cuando el valor booleano es falsofalse
Cuando es verdadero (true), el diagrama escalonado de la finción acumulativafda.
Ejemplo:
Hipergeométrica[10, 3, 5, x(A) > 0] grafica el histograma correspondiente a la acumulativo de valor aproximado 2.5 siendo la abscisa de A positiva y el unitario de la densidad de probabilidad en caso contrario.- Hipergeométrica[ <Población>, <Número de Éxitos>, <Tamaño de la Muestra>, <Valor de Variable>, <BooleanaAcumulativa> ]
- Siendo
Xla variable aleatoria de la distribución hipergeométrica y v el valor asignado, los resultados serían:
- P( X = v) si el valor booleano es falsofalse
- P( X ≤ v) si fuera verdadero.
Si el valor booleano es falsofalse da por resultado el valor de la función de densidad de probabilidadfdp de distribución hipergeométrica para las condiciones dadas (número de éxitos y probabilidad indicadas).
En caso contrario, el de la distribución acumulativa
Ejemplo:
El siguiente boceto ilustra animadamente el tipo de diagrama que se despliega según el valor de la variable booleana y acorde a los valores de los parámetros que varían de modo aleatorio.
El siguiente boceto ilustra animadamente el tipo de diagrama que se despliega según el valor de la variable booleana y acorde a los valores de los parámetros que varían de modo aleatorio.
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
En esta vistaasociada al Sistema de Computación Algebraica, solo opera la siguiente variante de sintaxis:
- Hipergeométrica[ <Población>, <Número de Éxitos>, <Tamaño de la Muestra>, <Valor de Variable>, <BooleanaAcumulativa> ]
Ejemplos:
Hipergeométrica[10, 3, 3, round(random()), x(A) > 0]puede dar como resultado aleatorio \frac{7}{24} en la Vista CAS o, según el valor que asuma el valor de la variable, 0.29 en la Algebraica.
Este valor se modifica según el de verdad de la booleana (abscisa de A positiva o no) y cada vez que se recalculan, pulsanbdo F9, los valores aleatorios.
Asumiendo que, sin devolución se seleccionan dos bolillas de un conjunto de 10 bolillas siendo un par de ellas negras...Hipergeométrica[10, 2, 2, 0, false]establece \frac{28}{45}, la probabilidad de no escoger ninguna bolilla negra,Hipergeométrica[10, 2, 2, 1, false]establece \frac{16}{45}, la probabilidad de escoger una bolilla negra,Hipergeométrica[10, 2, 2, 2, false]establece \frac{1}{45}, la probabilidad de no escoger ambas bolillas negras,Hipergeométrica[10, 2, 2, 3, false]establece 0, la probabilidad de escoger tres bolillas negras.Hipergeométrica[10, 2, 2, 0, true]establece \frac{28}{45}, la probabilidad de escoger cero (o menos) bolillas negras,Hipergeométrica[10, 2, 2, 1, true]establece \frac{44}{45}, la probabilidad de escoger una o menos, bolillas negras,Hipergeométrica[10, 2, 2, 2, true]establece 1, la probabilidad de escoger dos o menos bolillas negrasHipergeométrica[10, 2, 2, 3, true]establece 1, la probabilidad de escoger tres o menos, bolillas negras.
Nota: Ver también el comando HipergeométricaInversa.