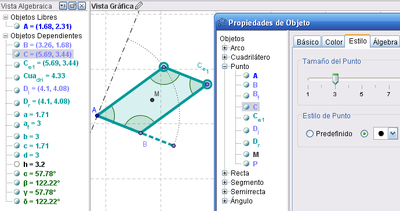
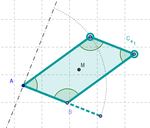
Paralelogramo a Cuadrado

Desafío: ¿Cómo harían para Dinamizar un Cuadrado?.
La Herramienta de Polígono regular permite construir un cuadrado, simplemente anotando un 4 frente a la caja de diálogo que solicita el ingreso del número de lados. Pero si se prefiere uno con mayores grados de libertad y acaso más versátil, conviene optar por otros pasos de construcción.
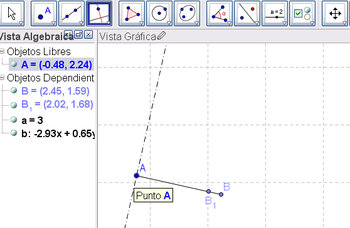
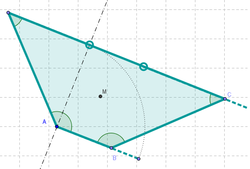
1 Crear un segmento, entre dos puntos, como A y B, en cualquier posición de la Vista Gráfica. Trazar la perpendicular al segmento entre A y B que pasa por A y un punto, digamos B1, en el segmento que une a A y B.
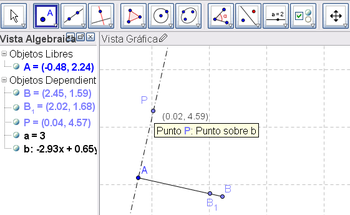
2 Crear un punto, digamos P, sobre esta perpendicular.
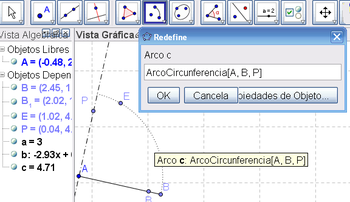
3 Emplear la Herramienta de Arco de Circunferencia para tender un arco con centro en A y extremos B y P (el punto sobre la perpendicular trazada) y crear un Punto sobre el arco creado .
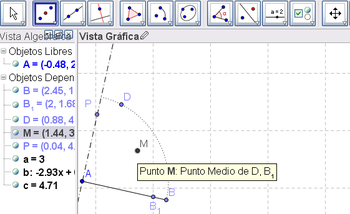
4 Con la Herramienta de Medio o Centro fijar el punto medio, digamos M, entre el punto sobre el arco y B_1.
5 Con la Herramienta de Simetría Central, reflejar A por M para obtener C.
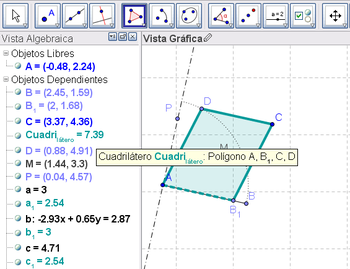
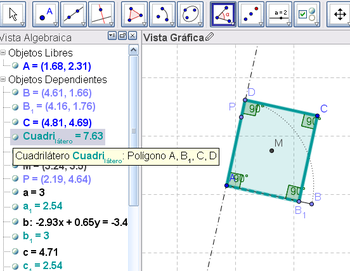
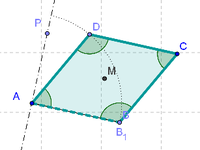
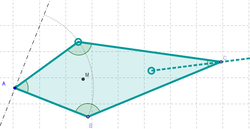
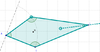
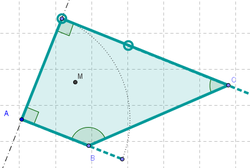
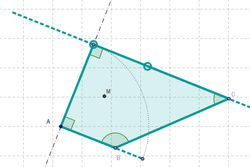
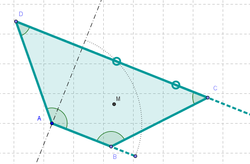
6 Unir con la Herramienta de Polígono los puntos A, B_1, C y D, de modo que si B_1 coincide con B, cuando D llega al extremo del arco, se forma un cuadrado (y un rombo si D ocupa cualquier otra posición intermedia).
7 Con la Herramienta de Ángulo aplicada sobre el polígono creado es posible verificar sus dimensiones y controlar si se está frente a distinto tipo de cuadrilátero.
8 Más allá de los diversos tipos de cuadriláteros a los que se puede llegar, este es un buen momento para explorar e indagar si hubiera otros que se puedan proponer.
- ¿El método que se emplee para lograr cada uno de los cuadriláteros de distinto tipo, será el único? ¿Será válido en todos los casos? ¿Cómo podríamos asegurarlo?
9 Con la Herramienta de Elige y Mueve y un control sobre la información que se vincula entre la que brinda la Vista Gráfica y la de las medidas presentes en la Vista Algebraica es posible verificar y relacionar dimensiones para controlar, más allá de la apreciación visual si se está frente a distinto tipo de cuadriláteros.
- ¿Habrá algunas metas imposibles de lograr? ¿Cómo podríamos convencernos de esta imposibilidad?
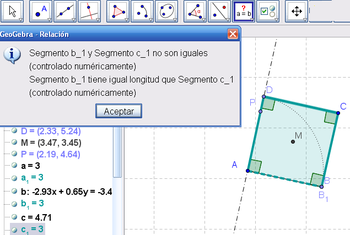
10 Con la Herramienta de Relación es posible verificar que se ha arribado a distinto tipo de cuadriláteros.
- ¿Cómo controlar que se llega a cada una de las metas propuestas? ¿Qué herramientas conviene emplear y qué relaciones verificar?
11 Un modo de ampliar la variedad de tipos de cuadriláteros a obtener de la exploración dinámica, podría surgir de proponerse que el punto D actual no sea sino uno de los extremos de una semirrecta sobre la que se puede deslizar ese cuarto vértice. Hasta podría, posteriormente, establecerse otro tanto para C. Para empezar, se cambia el estilo y nombre de sendos puntos, apelando al Cuadro de Propiedades.
12 Sobre los renovados puntos, se pasa a operar.
13 En primer lugar, obteniendo la semirrecta correspondiente a los trapecios.
14 Al hacer coincidir los lados que tienen en común el vértice A, lo que se logra llevando B al extremo, se pasa a trazar la semirrecta para obtener romboides.
15 Para ensayar los resultados, se debe crear un punto C en la semirrecta creada y apelar al Cuadro de Redefinición, emergente al dar doble clic sobre el objeto, para redefinir el cuadrilátero de modo que su tercer vértice pase a ser el "nuevo" punto C.
16 En síntesis, para lograr la ductilidad adicional que se propone, se empieza por determinar que la semirrecta por la que se desplace el tercer vértice dependa de la relación entre los lados que tienen A como vértice en común. Porque, si son iguales, conviene extender la semirrecta que permite pasar del rombo obtenido a toda la familia de posibles romboides.
17 Si no fueran iguales los lados que confluyen en A, convendría extender una semirrecta que permite pasar desde el paralelogramo obtenido a toda la posible serie de trapecios.
18 El ingreso implicado en la Barra de Entrada para la creación de esta dinámica semirrecta articula varios comandos...
- Semirrecta(C_{e_1}, Refleja[Si[Distancia[A, B) ≟ Distancia[A, D_r], A, Interseca[Recta[C_{e_1}, Recta[A, B_f]], Recta[A, P]]], C_{e_1}]]
19 Si se desea ampliar aún más el espectro dinámico de los posibles cuadriláteros, es posible extender un segmento que tendrá en el punto D original su extremo, para que tenga un recorrido de desplazamiento que permita el trazado preciso de un trapecio isósceles, llegado el caso.
20 Tal segmento puede trazarse apelando a una serie de herramientas que permitan establecer los correctos vectores que trasladen el punto D original al extremo que delimita los trapecios isósceles y luego poner esta traslación a prueba en sucesivas exploraciones.
21 Esta exploración puede compendiarse en la Barra de Entrada, incluso, para llegar por sucesivas maniobras de copiar y pegar para evitarse la creación de tantos objetos, en lo que resulta complicado pero no es más que la paciente unión de tal secuencia de pasos:
Si[¬(f ∥ Recta[A, B]), Segmento[D_r, Traslada[A, Distancia[A, B] VectorUnitario[Recta[A, D_r]]]], Segmento[D_r, Traslada[Traslada[A, Vector[B, Traslada[B, Distancia[B, Recta[C, Recta[A, B]]] VectorUnitarioPerpendicular[Recta[A, B]]]]], Vector[C, Traslada[B, Distancia[B, Recta[C, Recta[A, B]]] VectorUnitarioPerpendicular[Recta[A, B]]]]]]]
22 El boceto resultante puede ofrecerse a los estudiantes que, sin necesidad de pasar por el desafío de alto nivel operativo y de quehacer matemático involucrado, pasen a explorarlo para "ver cómo funciona" y establecer "cómo harían para... " lograr dejar trazadas las vistas representativas de cada tipo de cuadrilátero.
23 Con la Herramienta de Relación aplicada sobre los elementos cruciales es posible verificar que se registra en las mediciones lo que se aprecia "a ojo de buen cubero".
Sin menospreciar el intenso quehacer matemático de estas inspecciones, solo el análisis que se asiente sobre los conceptos figurales implicados pero los superen en un validación conceptual, compondrá una guía de trabajo completa.
Guía que será el desafío de organización matemática y didáctica que el docente que la diseñe tendrá por delante para pasar desde este boceto preparado para los estudiantes a un recurso genuino de indagación y clasificación.
Guía en que habrá que ...
- Establecer una serie de metas respecto de los cuadriláteros de diverso tipo a arribar
- Verificar que se trate de tales apelando a la manifestación de sus propiedades que se evidencia en cada una de las "vistas" y
- Controlar la generalidad de los procedimientos que se vayan encontrando
... en una indagación activa de exploración conceptual.