Comando Pascal

De GeoGebra Manual
Pascal
Categorías de Comandos (todos)
| Página en proceso de traducción. |
- Pascal[ <Número de Éxitos>, <Probabilidad de Éxito> ]
- Establece y grafica el histograma correspondiente a una distribución binomial negativa de Pascal (del inglés, Negative Binomial Distribution) para los valores paramétricos indicados.
Nota: El valor de la probabilidad debe restringirse al rango válido [0, 1].
Parámetros
- Número de Éxitos: número de intentos de Bernoulli independientes que deben ser positivos.
- Probabilidad de Éxito: valor de la probabilidad de éxito en cada ensayo.
- Pascal[ <Número de Éxitos>, <Probabilidad de Éxito>, <BooleanaAcumulativa> ]
- Si el valor booleano es falsofalse, establece y grafica, tomando x como variable, el histograma correspondiente a la fdp, función de densidad de probabilidad (en inglés, pdf)probabilty density function de la distribución binomial negativa de Pascal y el diagrama acumulativo correspondiente en caso contrario.
| Sintetizando... P( X = v) si el parámetro booleano fuera falso. P( X ≤ v) si fuera verdadero. |
Ejemplos:
El siguiente boceto ilustra animadamente el tipo de diagrama, de barras o escalonado acumulativo, que se despliega según el valor de la booleana y el de los restantes parámetros que también se modifican aleatoriamente.
Pascal[12, 0.75] da por resultado 0.98 y grafica el histograma correspondientePascal[12, 0.75, true] da 6.02 (acumulativo) y grafica el histograma correspondientePascal[1, 1/6, x(A) > 2] da 5.81 cuando la abscisa de A es mayor que 2 y 0.84 en caso contrario, presentando dinámicamente el diagrama acorde a la distribución acumulativa o no, en cada casoEl siguiente boceto ilustra animadamente el tipo de diagrama, de barras o escalonado acumulativo, que se despliega según el valor de la booleana y el de los restantes parámetros que también se modifican aleatoriamente.
| Se suma una alternativa que no desenvuelve histogramas Pascal[ <Éxitos>, <ProbabilidadÉxito>, <ValorVariable>, <Booleana> ] |
- Pascal[ <Número de Éxitos>, <Probabilidad de Éxito>, <Valor de Variablev>, <BooleanaAcumulativa> ]
- Si el valor booleano es falsofalse da para el valor v asignado a la variable, el de la función de densidad de probabilidadfdp de distribución binomial negativa de Pascal con parámetros indicados.
En caso contrario, el de la distribución acumulativa correspondiente.
Así, Pascal[e, p, v, booleana] da el valor para v de la fda de la distribución binomial negativa de Pascal para parámetros dados y variable aleatoria de distribución binomial negativa de Pascal igual a v.
En caso contrario, el de la distribución acumulativa.
Así, si fuera X la variable aleatoria y v el valor asignado, resultaría:- P( X = v) si el valor booleano fuera falso.
- P( X ≤ v) si fuera verdadero.
 En Vista CAS ComputaciónAlgebraicaSimbólica
En Vista CAS ComputaciónAlgebraicaSimbólica
Exclusivamente opera la variante previa que calcula el valor correspondiente:
- Pascal[ <Número de Éxitos>, <Probabilidad de Éxito>, <Valor de Variable>, <BooleanaAcumulativa> ]
| Sin diagramas, se opera también con literales |
Ejemplos:
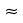 0.116decimales según Redondeo y al evaluarlo resulta
0.116decimales según Redondeo y al evaluarlo resulta 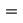 \frac{25}{216}
\frac{25}{216}
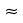 0.42 y es evaluado como
0.42 y es evaluado como 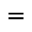 3 B {\left( 1, 3, \frac{1}{6} \right)}.
3 B {\left( 1, 3, \frac{1}{6} \right)}.
Operando con literales...
Pascal[12, 0.75] da por resultado 0.98Pascal[12, 0.75, true] da 6.02Pascal[12, 0.75, false] da 0.98Pascal[1, 1/6, 2, false] da el valorPascal[1, 1/6, 2, true] da como valor aproximado Operando con literales...
Pascal[1, p, 2, false] da por resultado p³ - 2p² + p Nota: En esta vista se admiten literales para evaluaciones simbólicas sujetas al valor dinámico de verdad de la variable booleana pero no se desenvuelven los diagramasSi se tildara el redondelito de encabezamiento de la fila, quedará representado el deslizador correspondiente al valor, no el histograma
Ejemplos:
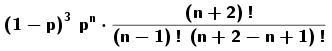
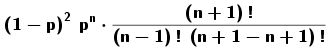
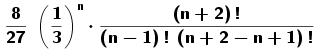
Siendo...
el número de éxitos en ensayos independientes de Bernoulli n = 1
la probabilidad de éxito p = \frac{1}{6}
el valor asignado a la variable es v = 2 y
falso (false) el valor booleno,
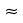 0.12decimales según Redondeo y al evaluarlo
0.12decimales según Redondeo y al evaluarlo 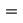 \frac{25}{216}
\frac{25}{216}
Pascal[ n, p, 3, false] da por resultado:Pascal[n, p, 2, x(A) > 2] da por resultado Ι(n, 3, p) cuando la abscisa de A es mayor que 2 y, en caso contrario,Pascal[n, 1/3, 3, false] da Siendo...
el número de éxitos en ensayos independientes de Bernoulli n = 1
la probabilidad de éxito p = \frac{1}{6}
el valor asignado a la variable es v = 2 y
falso (false) el valor booleno,
Pascal[n, p, v, false] da el valor 




